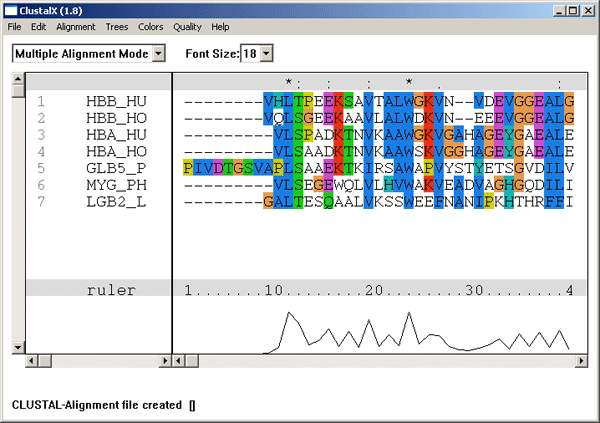
Our lab maintains and develops the Clustal Omega, Clustal W and Clustal X packages for multiple sequence alignment in collaboration with the groups of Toby Gibson at EMBL (http://www.embl-heidelberg.de/~gibson/), Julie Thompson in Strasbourg (http://www-igbmc.u-strasbg.fr/) and Rodrigo Lopez at the EBI (http://www.ebi.ac.uk). The package can be downloaded from the Clustal homepage (http://www.Clustal.org) or from the EBI ftp://ftp.ebi.ac.uk/pub/software/clustalw2/) or run on-line (http://www.ebi.ac.uk/Tools/msa/clustalo).
The package was recently revised and we released version 2.0 in Sept. 2007 (Larkin, et al, 2007). We are currently working on version 3.0 which we hope to release by 2010. The new work is funded by Science Foundation Ireland (http://www.sfi.ie) and will involve improving the accuracy of the alignments and the capacity to align very large data sets.
T-Coffee
T-Coffee (http://www.tcoffee.org/) was developed by and is maintained by Cedric Notredame (http://www.tcoffee.org/homepage.html ). It features a powerful and flexible approach to merging data from different sources to make high accuracy multiple sequence alignments of protein or nucleotide sequences. Our laboratory, collaborates with Cedric in the implementation and testing of T-Coffee for RNA alignment (R-Coffee, Wilm et al, 2008), protein structural alignments (3D-Coffee, O’ Sullivan, et al, 2003) and the merging of many multiple alignments (M-Coffee, Wallace, et al, 2006).
Multivariate Analysis of Omics Data
We have been applying a range of multivariate analysis methods to analyse high-dimensional genomics related datasets for some years. This work was initiated by Aedin Culhane (http://www.hsph.harvard.edu/research/aedin-culhane/) in our lab (now in the Dana Faber, in Boston) and with Guy Perriere
(http://pbil.univ-lyon1.fr/members/perriere/guy.html), Lyons, France, as collaborator. All of these data sets have a problem in that they usually have considerably more variables than cases and require careful selection of methods. In particular, we have been using Correspondence Analysis, Between Groups Analysis and Co-Inertia analysis and using the ADE4 R (http://pbil.univ-lyon1.fr/ADE-4/home.php?lang=eng ) package of Jean Thiolouse (http://pbil.univ-lyon1.fr/ADE-4/JTHome.html), in Lyons, France to apply these. ADE4 is free and has a huge range of clustering, ordination and discriminant methods.
We have applied these methods to e.g.
Sequence alignments (Wallace, et al, 2007)
Promoter motifs and gene expression data (Jeffery, et al, 2007)
Proteomics and gene expression data (Fagan, et al, 2007)
Cross platform gene expression data analysis (Culhane, et al, 2003)
A systematic exploration of the effect of guide-tree topology on
alignment quality for up to 8 sequences (and to a limited degree for
16 sequences) can be found in Fabian
Sievers et al, BMC Bioinformatics, October 2014, 15:338. There the
Supplement
contains a list of all rooted, toplologically distict, unlabeled,
bifurcating trees with up to 8 sequences. The number of different
rooted, toplologically distict, unlabeled, bifurcating trees is given
by the Wedderburn-Etherington
numbers. For 2 and 3 leaves there is only one possible tree, for 4
sequences there are 2 possible trees, for 5 there are 3, for 6 there
are 6, for 7 there are 11 and for 8 leaves there are 23 unlabeled
binary rooted trees. Tree shape can be summarised by the degree of
tree balance or imbalance. Some measures of tree im/balance are
defined in Shao, K., Sokal, R.: Tree balance. Systematic Zoology 39
(3), 266-276 (1990). Values for Tree Depth, Sackin's measure, Colless'
measure, Sokal's inv-max measure, Shannon Entropy and Tree Diameter
are given for up to 8 sequences in the Supplement. A
more complete list for up to 16 sequences can be found in the list of
all topologically
distinct trees with up to 16 leaves. This list also contains
values for the rescaled Sackin and Colless measures, the number of
sub-trees made up of exactly 2 leaves (cherries), the length of the
longest completely imbalanced/chained sub-tree (caterpillar) and the
number of symmetries (a,b) ⇔ (b,a), where a and b can be either
leaves or sub-trees themselves.
The expected values of the Sackin and the Colless measure under the
Equal Rates Markov or Yule (Yule et al., 1925) model, and the uniform
or Proportional to Distinguishable Arrangements model are shown in Fox
et al, Bioinformatics (2015).
Boyce et al have shown that 'Simple chained
guide trees give high-quality protein multiple sequence alignments',
PNAS 2014 ; July 9, 2014. Chained guide-trees are the most
imbalanced trees possible, where at each node at least one branch
subtends exactly one leaf.