| 
|
Between Group Eigen Analysis of Microarray Data | |
| Web Supplement |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Home
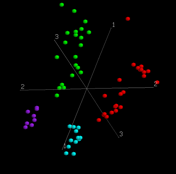
Takes you to our home page Figures figures from the paper Supplement Interactive figure 2 and 3 (Khan dataset) |
The effect of selecting genes on between group eigenanalysisBackground
Methods Two different metrics were used to select the genes that might be most useful for discriminating between the two groups. Genes were ranked using the t-statistic or the ratio of between-group to within-group sums of squares (BSS/WSS) for the two groups. The top 20, 50, 100, 200, 500, 1000 and 2000 genes were selected from each set of ranked genes in the training data and subjected to BGA using COA or PCA. The results of jack-knife experiments of these gene selections are shown in Table 1. Filtering of genes using either metric improved the assignment accuracy of data that had been subjected to BGA using PCA. In contrast filtering of genes using the BSS/WSS ratio reduced the prediction accuracy of the BGA/COA analysis. Taken on face value, this would suggest that BGA is best performed using PCA and that prior selection of at least some genes is useful. However repeating the above analyses using blind test data from Golub, et al. (1999) provides a more general and useful test. The 34 supplementary blind test samples from Golub, et al. (1999) were projected onto the discriminating axis produced from each of the gene selections above and the classification of each sample was assigned as AML or ALL (See results in Table 2). Using the full set of genes, the prediction accuracies were 82.4% and 88.2% respectively using BGA with PCA and COA. In the latter case all AML cases (15/15) and 16/20 ALL cases were correctly assigned (88.2%). Although there was a weak trend towards greater accuracy with smaller numbers of genes, the trend was highly variable depending on the ranking metric and the ordination method used. In general BGA using COA tended to out perform PCA ordination. Since COA has the further advantage that the genes and samples can be projected along the same axes, we only show results for BGA with COA in the paper. Tables Table 1 Percentage of correctly assigned training samples from the Golub, et al. (1999) data set in jackknifed tests when genes were ranked and selected using the t-statistic or BSS/WSS.
Table 2 Percentage of test samples from the Golub, et al. (1999) data set correctly assigned when genes were ranked and selected using the t-statistic or BSS/WSS ratio.
References
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||